Ship resistance and propulsion
A ship must be designed to move efficiently through the water with a minimum of external force. For thousands of years ship designers and builders of sailing vessels used rules of thumb based on the midship-section area to size the sails for a given vessel. The hull form and sail plan for the clipper ships, for, example evolved from experience, not from theory. It was not until the advent of steam power and the construction of large iron ships in the mid-19th century that it became clear to ship owners and builders that a more rigorous approach was needed.
Contents |
Definition
Ship resistance is defined as the force required to tow the ship in calm water at a constant velocity.
Components of resistance
A body in water which is stationary with respect to water, experiences only hydrostatic pressure. Hydrostatic pressure always acts to oppose the weight of the body. If the body is in motion, then there are also hydrodynamic pressures that act on the body.
|
|
|
|
|
|
|
|
Total resistance 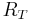 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
Residual resistance 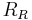 |
|
|
Skin friction resistance 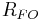 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
Form effect on skin friction |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
Pressure resistance 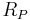 |
|
|
Friction resistance 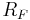 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
Wave resistance 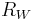 |
|
Viscous pressure resistance 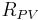 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Wavemaking resistance 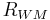 |
|
Wavebreaking resistance 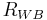 |
|
Viscous resistance 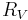 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
Total resistance 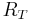 |
|
|
|||||||||||||||||||||
Froude's experiments
When testing ship models and then comparing the results to actual ships, the models tended to over predict the resistance of the ship.
Froude had observed that when a ship or model was at its so called Hull speed that the wave pattern of the transverse waves (the waves along the hull) have a period equal to the length on the water line. This means that the ship’s bow was riding on one wave crest and so was its stern. This is often called hull speed (the theoretical top speed of the ship) is a function of the length of the ship
V= 1.34√L
Observing this, Froude realized that the ship resistance problem had to be broken in to two different part: residuary resistance (wave making resistance) and frictional resistance. To get the proper wave making resistance, we need to recreate the wave train created by the ship on the model. He found that for any ship and corresponding model that:
to nondimensionalize it gravity was added in
There is a boundary layer that under goes shear at different rates extending from the hull surface until it reaches the field flow of the water. This can result in 50% of the total resistance in fast ship designs and 80 % of the total resistance in slower ship designs.
To account for the frictional resistance Froude decided to tow as series of flat plates and measure the resistance of these plates. This way you could take a plate with the same surface area as your ship model and back out the frictional resistance from the total resistance and what you have left is the residuary or wave making resistance.
Skin friction
In a viscous fluid, a boundary layer is formed. This causes a net drag due to skin friction. Further, because the ideal pressure now acts on the boundary layer, as opposed to the ship, and the boundary layer grows along the length of the ship, the net opposing forces are greater than the net supporting forces. This further adds to the resistance.
Wave-making resistance
A ship moving over the surface of undisturbed water sets up waves emanating from the bow and stern of the ship. The waves created by the ship consist of divergent and transverse waves. The divergent wave are observed as the wake of a ship with a series of diagonal or oblique crests moving outwardly from the point of disturbance. These wave were first studies by Lord Kelvin, who found that regardless to the speed of the ship, it always make a 19 degree angle to the wave. These waves produce little in the way of resistance against the ships forward motion. Transverse waves appear as troughs and crests along the length of a ship and constitute the majority of the wave-making resistance of a ship. The energy associated with the transverse wave system travels at one half the phase velocity or velocity of propagation of the waves. The prime mover of the vessel must put additional energy into the system in order to make up for this difference. The relationship between the ships velocity and that of the transverse waves can be found by equating the wave celerity and the ship’s velocity.
References
- E. V. Lewis, ed., Principles of Naval Architecture, vol. 2 (1988)